- Home
- Snow Information
- National Analyses
- Interactive Maps
- 3D Visualization
- Airborne Surveys
- Snowfall Analysis
- Satellite Products
- Forecasts
- Data Archive
- SHEF Products
- Science/Technology
- NOHRSC
- GIS Data Sets
- Special Purpose Imagery
- About The NOHRSC
- Staff
- NOAA Links
- Snow Climatology
- Related Links
- Help
- Help and FAQ
- Site Map
- Contact Us
- Please Send Us Comments!

|
Operational Automated Production of Daily, High-resolution,
Cloud-free Snow Cover Maps of the Continental U.S.
Core Science Demonstration for the GEWEX Continental-Scale International Project (GCIP)
Mississippi River Climate Conference, June 8-12, 1998, St. Louis, Missouri
Don Cline
Tom Carroll
National Operational Hydrologic Remote Sensing Center
National Weather Service, Office of Hydrology, NOAA
Abstract
Operational hydrology and meteorology
requires timely information about the distribution of snow cover for input
into forecasting models. Optical (visible and near-infrared) remote sensing
techniques have been used operationally for many years to provide snow
cover information. However, at any given time, large portions of the mapping
domain may be obscured by cloud cover. A method is required to infer the
presence or absence of snow cover beneath obscuring clouds.
We have developed a new data
assimilation strategy that uses a snow energy and mass balance model as
a basis for inference of snow cover when it is obscured to remote sensing
by cloud cover. The model accounts for snow surface and internal snow pack
energy exchanges, and mass exchanges including snow accumulation, sublimation,
rainfall, and melt water outflux. The snow energy and mass exchanges are
modeled hourly on a 4 km grid. Inputs to the model include analysis products
from the Eta model, satellite-derived insolation products from NESDIS,
and all available ground observations of precipitation. The modeled snow
water equivalence (SWE) is classified into a binary map of snow/no snow
using maximum likelihood logistic estimation, where the modeled SWE is
a continuous independent variable, and the binary dependent variable consists
of all available ground and airborne observations of snow depth and water
equivalence, and of samples of snow cover randomly selected from cloud-free
areas of a satellite snow cover product.
This approach permits the production of a snow cover map with five categories:
- snow cover directly observed by remote sensing,
- snow cover inferred under cloud cover,
- snow-free directly observed by remote sensing,
- snow-free inferred under cloud cover, and
- not mapped.
We demonstrate this approach
for the northwest quadrant of the GCIP NC-LSA (504,000 km2)
comprising most of Minnesota and the eastern Dakotas for a four week period
during March and April, 1997. Using the same modeled SWE as an independent
variable, tests of different data configurations in the logistic estimation
yielded overall classification accuracies ranging from 67-96% when compared
to ground snow observations and to remotely sensed snow cover. On average,
accuracies were highest (86-96%) during the first nine days of the study
period, prior to the passage of a major storm system that lasted several
days and included significant rainfall and snow accumulation. The lowest
accuracies (67-81%) were observed during the storm period.
1. Objective
Infer presence or absence of snow
cover beneath obscuring clouds, using information operationally available
in near-real time, to augment traditional remote sensing classification
of snow cover.
2. Background: Traditional Method
Cloud cover contamination represents
a significant constraint on traditional approaches of mapping the areal
extent of snow cover using optical (visible/near-infrared) remote sensing
data . In recent years there have been marked improvements in algorithms
designed to differentiate clouds from snow; however, no operational method
yet exists to reliably map snow cover beneath clouds at high spatial resolution
under a wide variety of snow pack conditions. Hence, snow cover maps produced
by traditional classification methods necessarily include a map category
for clouds (Figure 1).

Figure 1. Flowchart illustrating traditional supervised classification
of snow cover using remotely sensed data in the visible and near-infrared
regions of the electromagnetic spectrum. Since clouds are opaque in these
regions, the presence or absence of snow cover beneath clouds is unknown.
3. Overview of New Approach
We present an innovative new modeling
approach to estimate the spatial distribution of the presence or absence
of snow cover. This new approach can be used operationally to augment traditional
snow cover mapping where clouds are present. This approach consists of
two steps (Figure 2). First, a spatially distributed snow energy and mass
balance model is driven by various hydrometeorological data to estimate
the snow water equivalence (SWE) at any given time. The model should be
expected to provide an approximate representation of where there is and
is not snow, but for various reasons it is unlikely that it is exactly
correct. In particular, nonlinear processes involved in snow melt become
much more significant as the snow pack becomes very shallow; errors in
the model at this stage could substantially impact the modeled position
of the snow line. This problem is addressed by relating the modeled SWE
back to observed snow cover. The SWE estimated by the model is used
in conjunction with snow cover observations to estimate the probability
of the presence of snow cover.
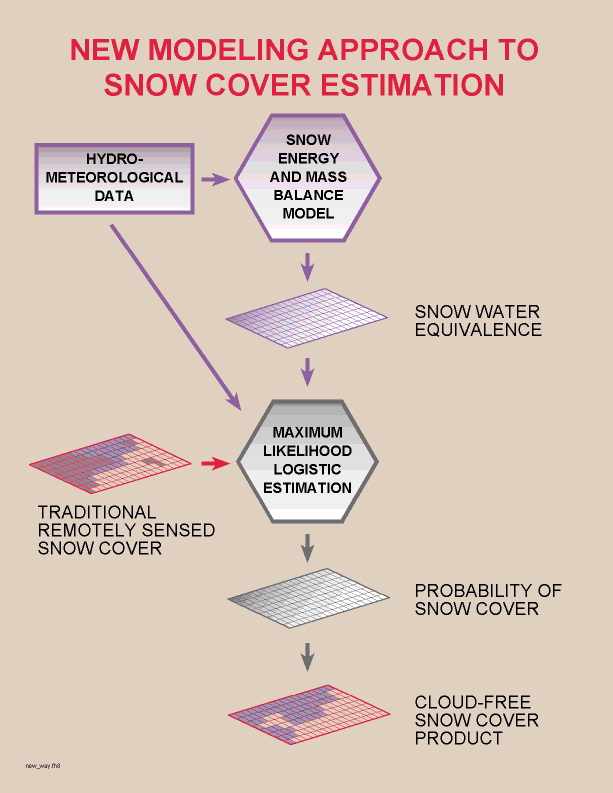
Figure 2. Flowchart illustrating the two major steps of the
new modeling approach: 1) snow energy and mass balance modeling to
estimate the spatial distribution of SWE, and 2) maximum likelihood logistic
estimation to relate modeled SWE and observed snow cover in order to estimate
the probability of snow cover.
The snow model is a spatially distributed
energy and mass balance model for a single-layer snow pack. It is based
in large part on the Utah Energy Balance Snow Accumulation and Melt Model
(UEB) (Tarboton and Luce, 1995), and on the snow energy and mass balance
model SNTHERM.89 (Jordan, 1991). The distributed model developed for this
approach accounts for mass exchanges of snow fall, rain fall, sublimation,
and snow melt outflux. It accounts for radiative and turbulent energy exchanges,
and includes parameterizations for forest cover effects (Figure 3). Model
state variables include the water equivalence of the snow pack and the
internal energy of the snow pack.
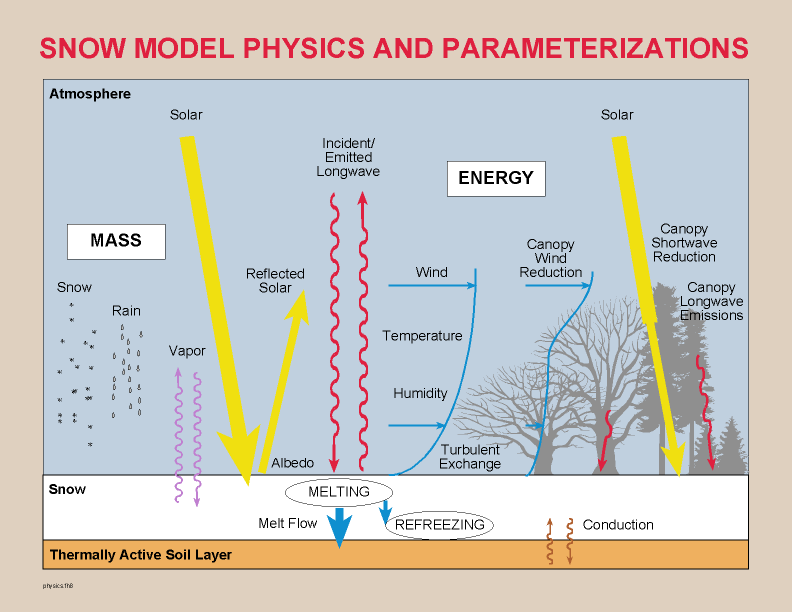
Figure 3. Snow model physics and associated parameterizations
for forest cover.
The estimation of the probability of snow cover involves
relating the SWE state variable of the model at time t to available
observations of the presence or absence of snow cover (Figure 4). Snow
cover observations may include ground-based or airborne-based observations
of SWE, ground-based observations of snow depth, and/or satellite observations
of snow cover where clouds do not obscure the surface. In the case of satellite
data, random samples of snow and no snow are drawn from the image-derived
snow cover map.
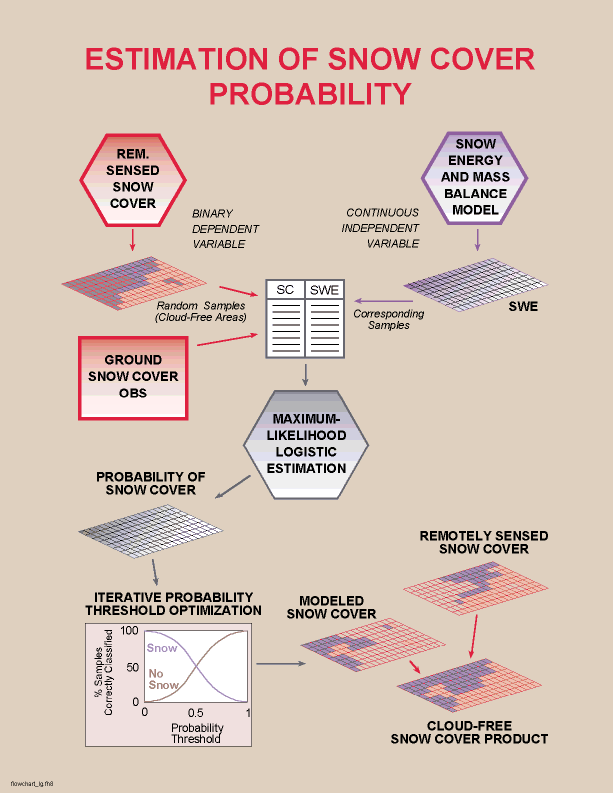
Figure 4. Flowchart illustrating inference of the presence or absence
of -snow cover based on probability of snow cover.
A set of snow cover observations and modeled SWE at corresponding
locations are input into a maximum likelihood logistic estimation (logit)
model. The logit model in turn estimates for each grid cell the probability
(0-1) that snow cover exists. The probability map is then classified
into snow or no snow by identifying a probability threshold that minimizes
the number of incorrectly classified observations and maximizes the number
of correctly classified observations. The final "cloud-free" snow cover
map consists of remotely sensed observations of snow cover where clouds
are not present, and the modeled snow cover beneath clouds.
4. Demonstration of New Approach
4.1 Methods
This approach was tested in a 504,000
km2 area of the northwest quadrant of the GCIP NC-LSA, which
includes most of Minnesota and the eastern Dakotas. This region is characterized
by relatively minor topography, with extensive forest cover throughout
northern Minnesota.
The model was run for a four-week period
from March 26, 1997 through April 22, 1997, which includes the major flooding
on the Red River of the North in the central part of the study area. This
time period includes three major snow pack/weather situations. The first
eight days (3/23 - 4/3) represents a "pre-storm period", during which no
significant precipitation occurred. During this first eight days, active
snow ablation was observed in the southern margins of the snow pack, with
the snow line receding northward. The second "storm period" occurred
during the next nine days from 4/4 through 4/12, during which time a series
of storm systems passed through the region. Significant precipitation resulted
from these systems, with the most notable event being a blizzard which
occurred while residents of the Grand Forks area were filling sand bags
in preparation for the 1997 Red River flood. The storm systems began as
a warm event, with widespread rainfall, which eventually turned to snow
in the northern part of the study area. Successive precipitation events
occurred during this period, with both snow pack ablation and accumulation
observed. The final "post-storm period" followed, from 4/13 through 4/22.
During this period, only scattered minor precipitation events were observed.
Ablation of the snow pack was widespread, with nearly complete ablation
observed throughout the study area by April 22.
Data to drive the snow model came from
three major sources: 1) 3-hourly analysis products from the NOAA
Eta atmospheric model , 2) hourly insolation products derived from the
NOAA GOES 8/9 satellites (Tarpley, 1997; Pinker, 1997), and 3) all available
ground precipitation observations within the study area from WFOs and cooperative
observers (Figure 5). The model was run at hourly temporal resolution and
4 km spatial resolution. Gridded input data were interpolated from relatively
coarse source grids to the 4 km grid, treating the source grids as a lattice
of points. Similarly, the ground observations of precipitation were simply
interpolated to a grid. Gridded forest cover and type information was derived
from AVHRR data (Zhu and Evans, 1994). Since for this demonstration it
was necessary to "cold-start" the model on 3/26/97, initial SWE conditions
were estimated using all available ground and airborne observations of
SWE, and all available snow depth observations. Co-located or neighboring
SWE and snow depth observations were used to estimate snow density in order
to relate snow depth observations to SWE.
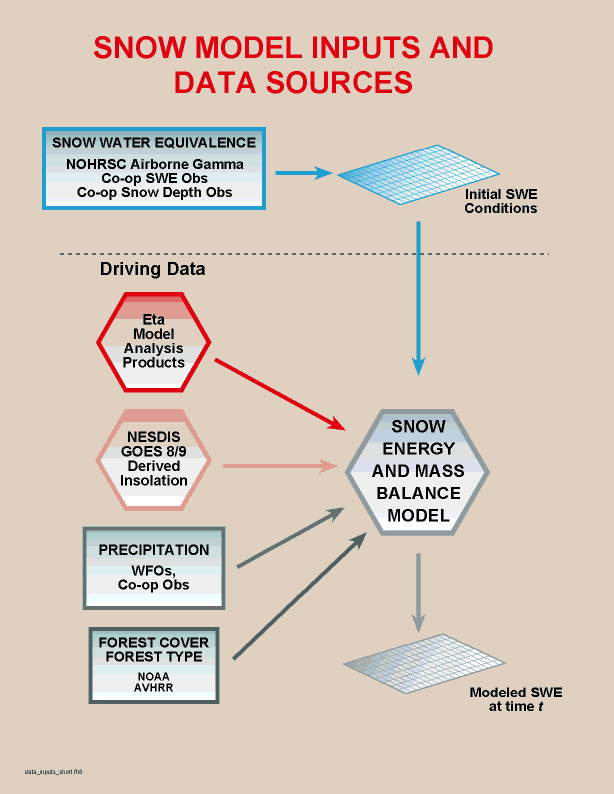
Figure 5. Flowchart illustrating data sources for distributed
snow model.
Two alternative snow cover data configurations
were tested for the probability estimation component of this approach:
-
only ground-based observations of snow cover (e.g. WFO and
cooperative observer observations of SWE or snow depth) were used in the
maximum likelihood logistic estimation. This simulates a "worst case" scenario,
where remotely sensed snow cover data are never available for an entire
month (e.g. continuous overcast conditions).
-
randomly sampled remotely sensed snow cover observations
are used when they were available (i.e. not obscured by clouds).
This simulates a more typical scenario, where a given location is temporarily
obscured by periodic cloud cover. Remotely sensed snow cover observations
were available for 17 of the 28 days of the study period form the National
Operational Hydrologic Remote Sensing Center (NOHRSC).
4.2 Results
The model representation of SWE during
the 28-day study period is shown in animation in Figure 6. In this figure,
the hourly modeled data are sampled every six hours. The view here is from
the southwest looking to the northeast.
.
Figure 6. Animation illustrating the modeled
spatial distribution of SWE throughout the study period.
A particularly interesting two day period (April 4 and
5) is shown at full hourly resolution in Figure 7. This period marks the
onset of the storm period. Relatively warm temperatures and widespread
rainfall resulted in rapid snow melt; subsequently, temperatures cooled
and the rain turned to snow, resulting in accumulation of the snow pack
in some areas. The model representation of SWE during this complex situation
is conceptually correct.
Figure 7. Hourly animation illustrating rapid
snow melt resulting from warm air temperatures and rain-on-snow, followed
by snow fall and accumulation of the snow pack.
The final "cloud-free" snow cover
maps produced using this approach consist of remotely sensed snow cover
observations where clouds are not present, and the modeled snow cover beneath
clouds. The accuracy of the methods described here was evaluated using
the raw modeled snow cover information optimally classified form the probability
estimates, prior to combining the remotely sensed and modeled information
into a single product. Accuracy was evaluated in two ways: 1)
using information from the optimal classification of snow cover probability
into presence or absence of snow cover (where the number of correctly and
incorrectly classified sample observations are precisely known), and 2)
by comparing remotely sensed snow cover to modeled snow cover, pixel-by-pixel,
in cloud-free areas, using a standard KHAT statistic. The latter method
does not indicate how well the model performs beneath cloud cover, but
the large sample size in cloud-free areas allows inference of the overall
accuracy of the model. The first method does include clouded as well as
cloud-free areas, but involves a smaller sample size.
Overall, classification accuracies
ranged from 67-96% agreement with observed snow cover, depending on the
data configuration (worst-case or typical) tested and the weather
situations described previously (pre-storm, storm, and post-storm). The
average accuracy of this approach for the worst case configuration (#1,
27 modeled products) was 76% agreement with observed snow cover. The average
accuracy of the typical configuration (#2, 16 modeled products, corresponding
to availability of remotely sensed snow cover) was 82% agreement with observed
snow cover. The accuracy varied between the three snow pack/weather situations
described above (pre-storm, storm, and post-storm) (Figure 8). In general,
accuracies were highest during the pre-storm period, and lowest during
the storm when only ground observations were used.
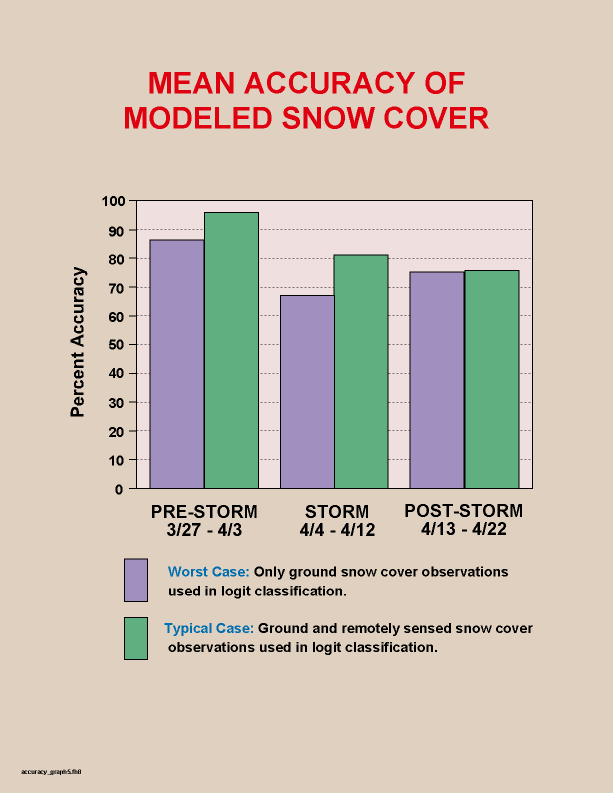
Figure 8. Mean accuracy of modeled snow cover for the three consecutive
snow pack/weather situations observed during the study period. The "worst
case" uses no remotely sensed data to develop the snow cover probability
estimate, simulating continuous overcast conditions. The "typical case"
uses a random sample of remotely sensed snow cover observations when they
are available.
The new "cloud-free" assimilated (modeled
under cloud, observed where cloud-free) snow cover map products generated
for this demonstration are listed below in Table 1, together with the corresponding
traditional NOHRSC snow cover products. These may be viewed and compared
by selecting the appropriate date in the table. The percentage of the satellite
image that was contaminated by cloud cover is shown in column two. The
model accuracy for the typical case described above is shown in column
three. This is the percentage of the snow cover observations, both ground-based
and satellite based, that were correctly classified following the identification
of the optimum probability threshold. The "Overall Agreement", "Commission
Error", and "Omission Error" columns result from a pixel-to-pixel comparison
of the model-estimated snow cover to satellite-observed snow cover wherever
there are not clouds. The Overall Agreement in column four is
the percentage of cloud-free pixels that were correctly classified by the
model. The Commission Error is the percentage of pixels where no
snow cover was observed by satellite but the model estimated to be snow-covered.
The Omission Error is the percentage of pixels where snow was observed
by satellite but the model estimated to be snow-free. The assimilated products
shown for each date only use modeled snow cover only under clouds, i.e.
those areas which are not reflected in the overall agreement or the commission
and omission errors. However, these values do provide some measure of how
accurate the inferred snow cover under clouds may be.
Table 1. Traditional satellite-derived snow cover maps produced
by the NOHRSC and the corresponding assimilated snow cover products.
All products are for 1600 UTC of the date indicated.
| Date |
Amount of Cloud Cover
in Image (%) |
Typical Case Model Accuracy (%) |
Overall Agreement (%) |
Commission Error (%)> |
Omission Error (%) |
|
March 27, 1997
|
21
|
94.3
|
90.6 |
2.8
|
6.5
|
|
March 31, 1997
|
0
|
96.0
|
90.4
|
4.4
|
5.2
|
|
April 1, 1997
|
31
|
92.4
|
88.9
|
4.9
|
6.2
|
|
April 2, 1997
|
86
|
98.8
|
99.9
|
0.1
|
0.0
|
|
April 3, 1997
|
25
|
97.0
|
92.0
|
5.3
|
2.7
|
|
April 7, 1997
|
55
|
75.1
|
56.3
|
0.0
|
43.7
|
|
April 8, 1997
|
53
|
86.0
|
71.3
|
0.0
|
28.7
|
|
April 9, 1997
|
31
|
81.8
|
73.5
|
1.0
|
25.5
|
|
April 13, 1997
|
0
|
82.9
|
77.0
|
3.5
|
19.5
|
|
April 14, 1997
|
21
|
77.0
|
73.7
|
7.4
|
18.8
|
|
April 15, 1997
|
86
|
69.4
|
63.3
|
4.4
|
32.3
|
|
April 16,1997
|
21
|
91.9
|
86.3
|
7.9
|
5.8
|
|
April 17, 1997
|
31
|
80.3
|
86.0
|
11.5
|
2.5
|
|
April 19, 1997
|
51
|
83.3
|
78.7
|
20.6
|
0.7
|
|
April 20, 1997
|
70
|
68.1
|
70.1
|
26.6
|
3.3
|
|
April 21, 1997
|
51
|
56.7
|
65.4
|
32.1
|
2.5
|
|
April 22, 1997
|
41
|
71.5
|
80.7
|
18.7
|
0.6
|
For discussion purposes, we compare
two particular series of traditional and assimilated snow cover products,
with each series consisting of three consecutive days. The first series
includes April 1, 2, and 3, during the pre-storm period (Figure 9). On
April 1, 30% of the traditional satellite-only snow cover map is
contaminated by patchy cloud cover. Based on the optimal classification
results, the modeled 4/1 snow cover is 81% correct for the worst
case and 92% correct for the typical case. On April 2, 85% of the
traditional satellite-only snow cover map is contaminated by cloud cover.
The 4/2 assimilated product is therefore almost entirely dependent on the
modeled snow cover. The areal extent of snow cover portrayed by the assimilated
product is approximately consistent with the previous and following days.
The worst-case accuracy for the assimilated 4/2 product is 87% when compared
to ground observations.
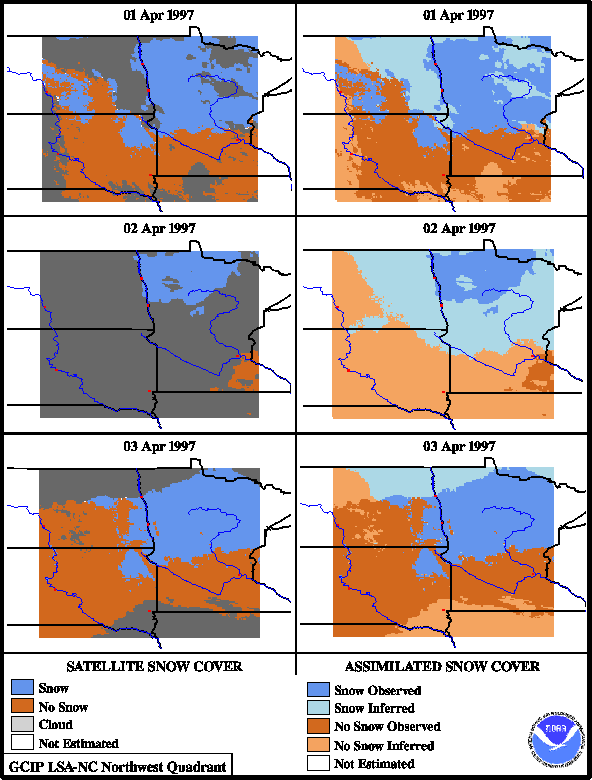
Figure 9. Comparison of traditional snow cover products
with assimilated product for April 1-3, 1997.
The second series includes April 14,
15, and 16, just after the storm period has passed (Figure 10). Once again,
almost complete (86%) overcast conditions were observed in the traditional
satellite-only snow cover map for April 15. On April 14, snow cover was
observed by satellite throughout central and southern South Dakota and
northern Nebraska, with fairly extensive cloud cover throughout most of
North Dakota. The worst-case accuracy for 4/14 is 70%, and the typical-case
accuracy is 77%. The assimilated product for 4/15 is again dependent almost
entirely on modeled snow cover due to the extensive overcast conditions.
The model indicates that the snow cover in central South Dakota and northern
Nebraska present the previous day has ablated. The worst-case accuracy
of the 4/15 assimilated product is 77%, and typical case accuracy is lower
at 69%. However, the satellite-observed snow cover on the following day
does reveal that the snow cover throughout most of central South Dakota
and northern Nebraska has indeed ablated. Although the exact timing
of this widespread ablation cannot be determined from available observations,
these results do suggest that the modeled snow cover is reasonable.
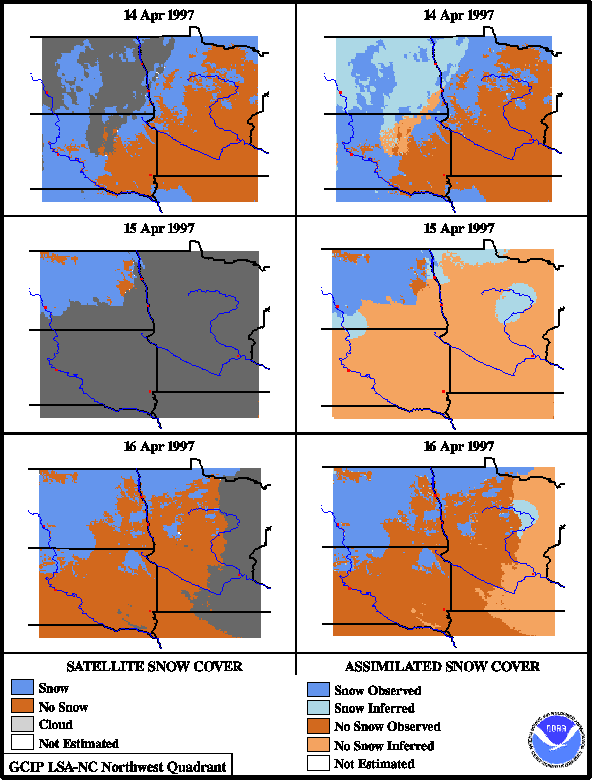
Figure 10. Comparison of traditional snow cover products
with assimilated product for April 14-16, 1997.
5. Conclusions
This approach to inferring the presence
or absence of snow cover beneath clouds is promising. All data used to
drive the snow model are available operationally in near-real time. The
snow model includes the major physical processes involved in snow accumulation
and melt, but remains a relatively simple, parsimonious model for snow
energy and mass exchanges. Consequently, the model is computationally tractable
at relatively high spatial resolutions over large areas.
The overall accuracies of the modeled
snow cover information are comparable to accuracies typically attainable
by traditional remote sensing classification of snow cover. The assimilated
snow cover products demonstrated here use remotely sensed snow cover where
clouds are not present, and only employ the modeled snow cover beneath
clouds. The comparable accuracies of the two methods suggests that
augmentation of operational satellite remote sensing of snow cover with
this new approach in an automated framework would not result in a significant
loss of accuracy. Moreover, this approach potentially permits more frequent
(e.g. daily) production of snow cover maps that reaonably infer
snow cover beneath clouds.
6. References
Jordan, R., 1991. A one-dimensional temperature model
for a snow cover, Spec. Rep. 91-6, U.S. Army Cold Regions Research
and Engineering Laboratory, Hanover, NH.
Pinker, R.T., and I. Laszlo, 1992. Modeling surface solar
irradiance for satellite applications on a global scale, Journal of
Applied Meteorology, 31, 194.
Tarboton, D., and C. Luce, 1996. "Utah Energy Balance
Snow Accumulation and Melt Model (UEB)," Computer model technical description
and users guide, Utah Water Research Laboratory and USDA Forest Service
Intermountain Research Station.
Tarpley, D., 1998. Personal communication.
Zhu, Z., and D.L. Evans, 1994. U.S. forest types and predicted
percent forest cover from AVHRR data, Photogrammetric Engineering and
Remote Sensing, 60(5), 525-531.
|





